さて、今回は数学の入門書からピックアップいたします。

それがこちら。

『数学が生まれる物語』１～６、志賀浩二 著、2013年、岩波書店

です。

「数学が生まれる物語」は、題名から数学史の本かと思いきや、がっつりとした数学の入門書。

数とは一体何か。数学をより身近なものとして理解できるよう、数についての根本的な概念から数学の考え方をやさしく解説しています。理解しているようで理解できていなかった数学を基礎から学びなおすための本です。

著者の志賀浩二氏は中学生の時のふとしたきっかけから数学に没頭するようになり、東京大学大学院数物系修士課程を修了。その後は東京工業大学理学部数学科教授、桐蔭学園横浜大学工学部教授、桐蔭生涯学習センター長などを務め、現在、東京工業大学名誉教授です。

ちなみに東京工業大学理学部数学科教授を早期退職したのは「無限がわからなくなった」ということが理由だそうです。数学を理解できていないわたしにはちょっとよくわからないですね…。

著書として、自身の専門である「多様体論」といった学術書だけではなく、この本をはじめとして『数学30講シリーズ』（全10巻、朝倉書店）や『中高一貫数学コース』（全11巻）、『算数から見えてくる数学』（全５巻、以上、岩波書店）といった数学の入門書シリーズを多数執筆しています。その著書はなんと100冊以上。さらに、2005年（平成17年）には「数多くの数学啓発書の執筆および編集により数学の研究・教育・普及に大きく貢献」したことを評価されて第1回日本数学会出版賞を受賞しています。

本書はそんな数学をこよなく愛する著者が昨今の数学離れを憂えて、あらゆる年齢層と知識レベルに向けて精力的に書き続けている副読本のシリーズとなります。

各巻の内容について

このシリーズは全6巻構成になっています。ここからは各巻の内容について見ていきましょう。

第1週　数の誕生

第1週では、数学学習の第一歩として、まず自然数、分数、小数を学びます。数とは一体何か。数についての根本的な概念や、数学の考え方をやさしく解説。数学をより身近なものとして理解できるよう、数の持つさまざまな姿を示します。

【写真1】第1週p3より。リンゴが3個、木を植えてから3年、オリオン座の3連星。それらに共通する抽象的概念「3」を抽出して捉えることは実は当たり前ではなく長い歴史が必要とされました。

第2週　数の世界

第2週では負の数、有理数、実数や、数の計算法も整理された形で学びます。「無限」と「連続」という互いに映しあう2つの考えを通して、数学の奥深い世界を理解することができるでしょう。

【写真2】第2週p94より。数直線とは何かを最初に考えたドイツの数学者デデキントに触れます。左に配置されたイラストや似顔絵に和まされます。

第3週　式と方程式

第3週では、数の四則演算が発展して生まれた代数について学びます。いよいよ実数から複素数へ。2次方程式の解の公式や判別式なども登場します。

【写真3】整数とは？有理数とは？こちらのページの図は数の世界の広大さを改めて教えてくれます。

第4週　座標とグラフ

第4週の舞台は座標平面、主人公は関数とグラフです。関数は座標平面の上でグラフ表示され、これまでの代数の世界とは異なる躍動する数学の世界が展開されます。

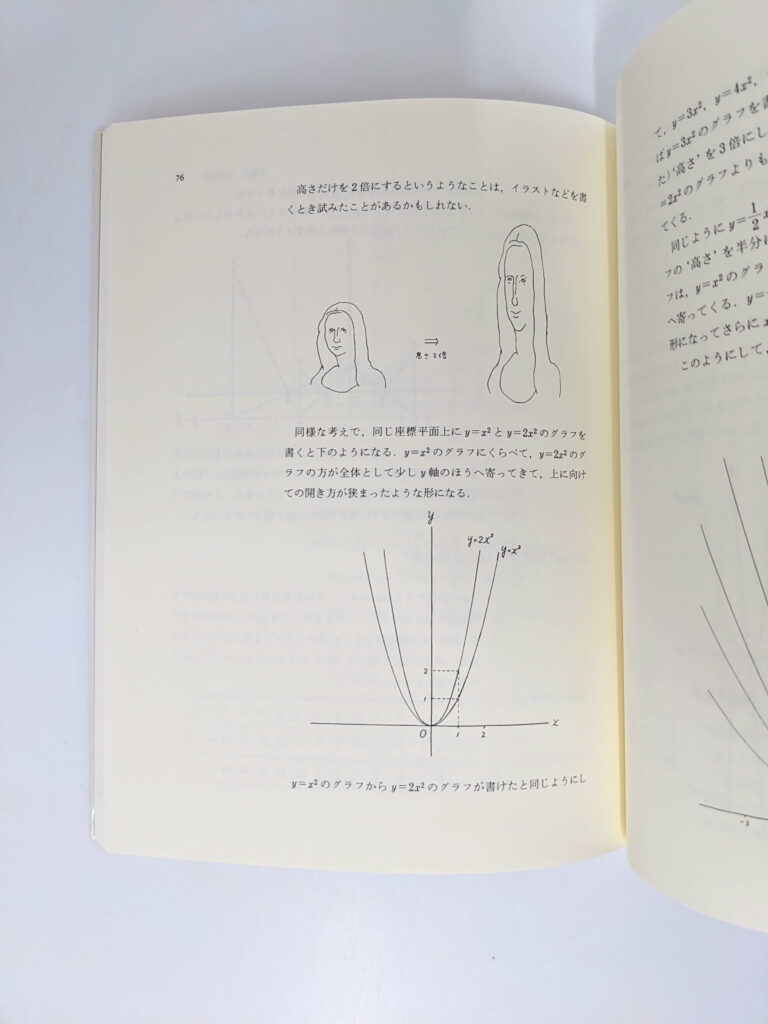
【写真4】高さが2倍になったモナリザ。インパクト大ですが、2次関数の係数によりグラフがどう変化するのか印象に残ります。

第5週　関数とグラフ

第5週では、関数を分析する一般的な方法として微分について学びます。そして３次関数、三角関数、指数関数などに適用し、これらのいろいろな性質を調べていきます。

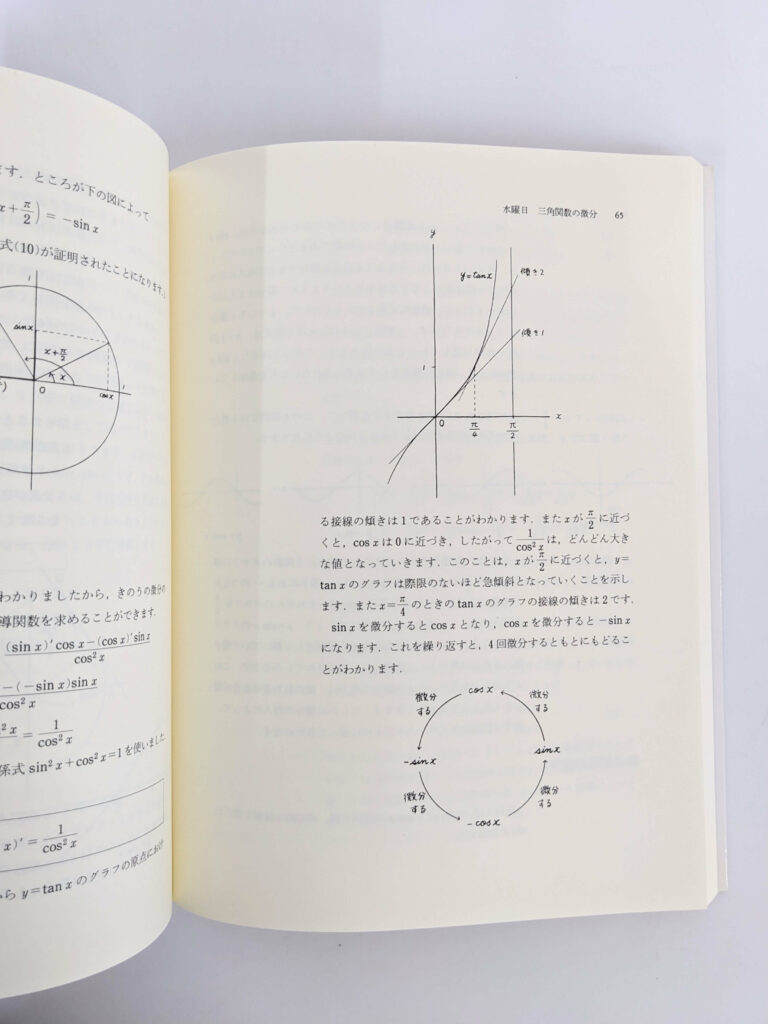
【写真5】第5週、「三角関数の微分」p65より。sin、cos、tanの関連がどうなっているのか、視覚的にも分かりやすく説明されています。

第6週　図形

「数学が生まれる物語」の最後の週は、平面幾何、解析幾何、図形の面積や体積を求める積分について学びます。図形を通して方程式、関数、微分、積分などの考えが総合され、多彩な数学の世界が展開されます。

【写真6】最終週の「土曜日」ともなると、今までの集大成の様相を呈してきます。

このシリーズは、中学から高校初年級の数学を分かりやすい文章とたくさんの味のある挿絵によってやさしく説明しています。

第1週から第6週まで各巻1週間で読むことができる構成となっており、章立てが曜日となっています。月曜日から土曜日までは授業風景を取り入れた講義形式で、週の最後の日曜日にはピタゴラスの定理やパスカルの三角形など興味深いトピックを紹介しています。

【写真7】第3週「日曜日」より、「パスカルの三角形」。ここに至るまでの説明数ページは是非お手にとってご確認ください。

内容としては非常に濃いですが、1日1章という目安があるのでペースを保って読むことができます。文字を追うだけでは分かりづらい人は、ノートを傍らにおいて実際に講義を受けるようにまとめていきましょう。講義の最後には問題があります。終わった後に解いてもいいし、次の日の章を読む前に確認として解くのもいいでしょう。

本書を一通り読破すれば、学校で習う基礎的な数学を１から学びなおすことができます。

これから数学を学ぶ人の必読書

数【すう】

物の多少、大小、位置、順序などを表すために考えられた仕組みで、その目的から生まれた自然数、整数、有理数、実数、複素数などの総称。単に数というときは、前後の文脈によって自然数だけをさすこともあり、また、もっと広く有理数や実数や複素数まで考えていることもある。物に数を対応させることを、数える（最小の単位になるものがあって、それらが集まっている場合）とか、測る（最小の単位がない場合）とかいうが、数という語は、数えたり、測ったりした結果得られるものをさすときにも用いられる。

日本大百科全書（ニッポニカ）より引用

今日、私たちの周りにはたくさんの数が飛び交っています。しかし、あなたは「数とは何か」と聞かれたら、上記に書いてあるようなことをはっきり答えることができるでしょうか。普通の人は「数とは何か」というようなことは考えずに生活しています。少なくとも、この文章を書いている私自身は答えることができませんでした。

私たちは幼いころから、ひとつ、ふたつ、みっつ…と数えることを知っていました。しかし、その理解は無意識かつ感覚的なもので、あえてそれを論理的に言語化することは基本的にしないでしょう。そんなことをしなくても生活はできますし、学校で習う算数や数学のレベルにはついていけます。しかし、それ以上の高等数学を学ぼうと思うと必ずこの「数の性質」についての理解が重要になってきます。

本書をとりあえずざっと読んで一番驚いたことは、自分は数学の基礎的な知識が全然身についていなかったこと。

私は今でこそ文系の人間ですが、高校のはじめまで数学が得意科目のひとつでした。数学ⅠAのあたりだったら、模試でも8割とれていたくらい。しかし、高校2年になり数学ⅡBに駒をすすめると、途端にいままで苦労せずに解けていた問題が一気に分からなくなったのです。教科書を読んでも、いまいち理解ができない。使う公式がある程度決まっている定期試験は何とかパスできていたけれど、受験対策の応用問題はチンプンカンプン。この本を読んで、私はそれまで得意だと思っていた数学の基礎が全然できていなかったことに気づかされました。ここまで理解できていなかったら躓くはずだと妙に納得しています。

数学の勉強というと、まず公式を覚えてあとはひたすら問題を解くという流れになりますよね。授業で定義や定理、公式はひととおり学びますが、後のテストで必要なのは「この問題だったらこの公式を使う」というパターンを叩き込むこと。それが何を意味するのかについてはほとんど教わらず、空虚な公式しか頭に残らないのです。

高校までの数学だったらそのままでも問題はないでしょう。しかし、この数学の基礎を根本的に理解していないと、大学で学ぶ数学のようなより専門的な数学は意味不明になってしまいます。実際、それで挫折する人も多いようです。

そのため、あいまいになった数の性質から方程式、グラフや図形まで小学校から高校までに習う基本的な数学の基礎を懇切丁寧に解説し、再学習できる本書は「数学を学ぶ人の必読本」といえるのです。

【写真8 】各週の巻頭に付された「読者へのメッセージ」。著者が本シリーズを「数学が生まれる物語」と命名した数学への愛がこの文章には詰まっています。

まとめ

私たちが何かを覚えたい、やりたいと思う時に最初にやるべきことは基礎の習得です。そのことをこの本はあらためて教えてくれました。

これは数学だけでなく、他の学問やスポーツ、音楽にしてもいえることです。基礎を学ぶ理由は、なんといっても「強固な土台を築くため」と言えます。基礎を強固な土台として作り上げることで、より高い到達点に挑むことができるようになり、多様性や柔軟性を養うことができます。一方、この土台が出来ていないとある程度は積み上げることができたとしても、どこかで破綻します。

もしかしたらずっとニガテだと思っていた科目は実は基礎があいまいだったからかもしれません。どうしても基礎が理解できない場合は、理解できるまで何度も反復するといいでしょう。諦めずに何度も基礎を勉強することで、無意識化に落とし込むことができます。

とりあえず、高校で習った数学に対するニガテ意識がぬぐえない私はしっかりとこの本で数学の基礎を叩き込もうと思います。そうしたらずっといまいち理解できなかった命題の真偽とか微分・積分、ベクトルとかにあらためて挑戦してみたいと思った読後でした。

【本シリーズのご購入はこちらから】